Heuristic search is a very general method applicable to a large class of problems. It encompasses a variety of specific techniques, each of which is particularly effective for a small class of problems. In order to choose the most appropriate method (or combination of methods) for a particular problem, it is necessary to analyse the problem along several key dimensions:

I. Is the problem decomposable into a set of (nearly) independent smaller or easier sub problems?

II. Can solution steps be ignored or at least undone if they prove unwise?

III. Is the problem's universe predictable?

IV. Is a good solution to the problem obvious without comparison to all other possible solutions?

V. Is the desired solution a state of the world or a path to a state?

VI. Is a large amount of knowledge absolutely required to solve the problem, or is knowledge important only to constrain the search?

VII. Can a computer that is simply given the problem return the solution, or will the solution of the problem require interaction between the computer and a person?

Notice that some of these questions involve not just the statement of the problem itself but also characteristics of the solution that is desired and the circumstances under which the solution must take place.

1.1 Is the Problem Decomposable?

Suppose we want to solve the problem of computing the expression.

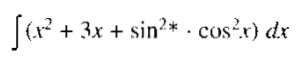
We can solve this problem by breaking it down into three smaller problems, each of which we can then solve by using a small collection of specific rules.

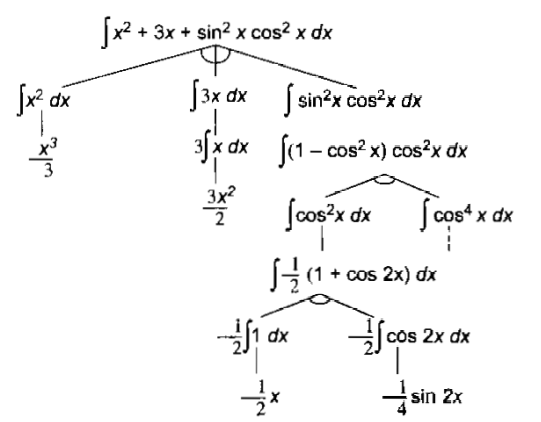
Fig: A Decomposable Problem

The above Figure shows the problem tree that will be generated by the process of problem decomposition as it can be exploited by a simple recursive integration program that works as follows: At each step, it checks to see whether the problem it is working on is immediately solvable. H so, then the answer is returned directly. If the problem is not easily solvable, the integrator checks to see whether it can decompose the problem into smaller problems. If it can, it creates those problems and calls itself recursively on them. Using this technique of problem decomposition, we can often solve very large problems easily.

1.2 Can Solution Steps Be Ignored or Undone?

Suppose we are trying to prove a mathematical theorem. We proceed by first proving a lemma that we think will be useful. A lemma that has been proved can be ignored for next steps as eventually we realize the lemma is no help at all.

Now consider the 8-puzzle game. A sample game using the 8-puzzle is shown below:

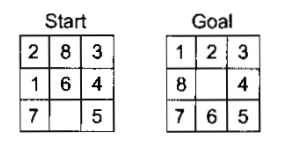
Fig: An Example of the 8-Puzzle

In attempting to solve the 8 puzzle, we might make a stupid move for example; we slide the tile 5 into an empty space. We actually want to slide the tile 6 into empty space but we can back track and undo the first move, sliding tile 5 back to where it was then we can know tile 6 so mistake and still recovered from but not quit as easy as in the theorem moving problem. An additional step must be performed to undo each incorrect step.

Now consider the problem of playing chess. Suppose a chess playing problem makes a stupid move and realize a couple of moves later. But here solutions steps cannot be undone.

The above three problems illustrate difference between three important classes of problems:

1) Ignorable: in which solution steps can be ignored. Example: Theorem Proving

2) Recoverable: in which solution steps can be undone. Example: 8-Puzzle

3) Irrecoverable: in which solution steps cannot be undone. Example: Chess

The recoverability of a problem plays an important role in determining the complexity of the control structure necessary for problem solution.

Ignorable problems can be solved using a simple control structure that never backtracks. Recoverable problems can be solved by slightly complicated control strategy that does sometimes make mistakes using backtracking. Irrecoverable problems can be solved by recoverable style methods via planning that expands a great deal of effort making each decision since the decision is final.

1.3 Is the universe predictable?

There are certain outcomes every time we make a move we will know what exactly happen. This means it is possible to plan entire sequence of moves and be confident that we know what the resulting state will be. Example is 8-Puzzle.

In the uncertain problems, this planning process may not be possible. Example: Bridge Game - Playing Bridge. We cannot know exactly where all the cards are or what the other players will do on their turns.

We can do fairly well since we have available accurate estimates of a probabilities of each of the possible outcomes. A few examples of such problems are

I. Controlling a robot arm: The outcome is uncertain for a variety of reasons. Someone might move something into the path of the arm. The gears of the arm might stick.

II. Helping a lawyer decide how to defend his client against a murder charge. Here we probably cannot even list all the possible outcomes, which leads outcome to be uncertain.

1.4 Is a Good Solution Absolute or Relative?

Consider the problem of answering questions based on a database of simple facts, such as the following:

1) Marcus was a man.

2) Marcus was a Pompeian.

3) Marcus was born in 40 A.D.

4) All men are mortal.

5) All Pompeian's died when the volcano erupted in 79 A.D.

6) No mortal lives longer than 150 years. 7) It is now 1991 A.D.

Suppose we ask a question "Is Marcus alive?" By representing each of these facts in a formal language such as predicate logic, and then using formal inference methods we can fairly easily derive an answer to the question.

Since we are interested in the answer to the question, it does not matter which path we follow. If we do follow one path successfully to the answer, there is no reason to go back and see if some other path might also lead to a solution. These types of problems are called as "Any path Problems".

Now consider the Travelling Salesman Problem. Our goal is to find the shortest path route that visits each city exactly once

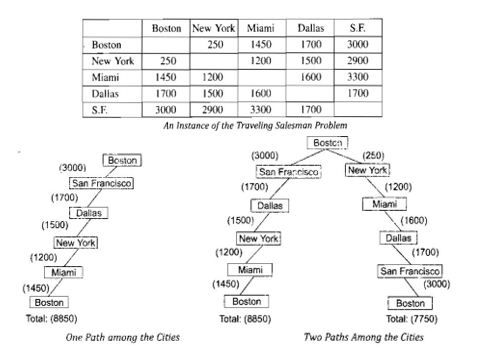
Suppose we find a path it may not be a solution to the problem. We also try all other paths. The shortest path (best path) is called as a solution to the problem. These types of problems are known as "Best path" problems. But path problems are computationally harder than any path problems.

1.5 Is the solution a state or a path?

Consider the problem of finding a consistent interpretation for the sentence

The bank president ate a dish of pasta salad with the fork

There are several components of this sentence, each of which may have more than one interpretation. Some of the sources of ambiguity in this sentence are the following:

I. The word "Bank" may refer either to a financed institution or to a side of river. But only one of these may have a President.

II. The word "dish" is the object of the word "eat". It is possible that a dish was eaten.

III. But it is more likely that the pasta salad in the dish was eaten.

Because of the interaction among the interpretations of the constituents of the sentence some search may be required to find a complete interpreter for the sentence. But to solve the problem of finding the interpretation we need to produce only the interpretation itself. No record of the processing by which the interpretation was found is necessary. But with the "water-jug" problem it is not sufficient to report the final state we have to show the "path" also.

So the solution of natural language understanding problem is a state of the world. And the solution of "Water jug" problem is a path to a state.

1.6 What is the role of knowledge?

Consider the problem of playing chess. The knowledge required for this problem is the rules for determining legal move and some simple control mechanism that implements an appropriate search procedure.

Now consider the problem of scanning daily newspapers to decide which are supporting 'n' party and which are supporting 'y' party. For this problems are required lot of knowledge.

The above two problems illustrate the difference between the problems for which a lot of knowledge is important only to constrain the search for a solution and those for which a lot of knowledge is required even to be able to recognize a solution.

1.7 Does a task require interaction with the person?

Suppose that we are trying to prove some new very difficult theorem. We might demand a prove that follows traditional patterns so that mathematician each read the prove and check to make sure it is correct. Alternatively, finding a proof of the theorem might be sufficiently difficult that the program does not know where to start. At the moment people are still better at doing the highest level strategies required for a proof. So that the computer might like to be able to ask for advice.

For Example:

I. Solitary problem, in which there is no intermediate communication and no demand for an explanation of the reasoning process.

II. Conversational problem, in which intermediate communication is to provide either additional assistance to the computer or additional information to the user.

Algorithm:

1. Start with OPEN containing just the initial state

2. Until a goal is found or there are no nodes left on OPEN do:

a. Pick the best node on OPEN

b. Generate its successors

c. For each successor do:

i. If it is not been generated before, evaluate it, add it to OPEN and record its parent.

ii. If it has been generated before, change the parent if this new path is better than the previous one. In that case update the cost of getting to this node and to any successors that this node may already have.

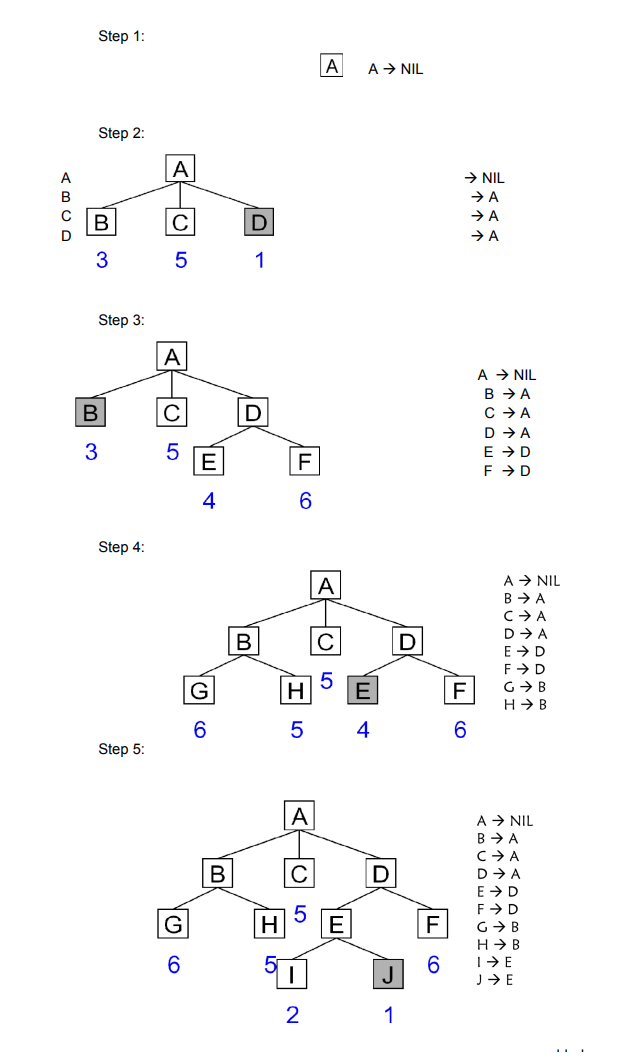
Problem Reduction:

I. Planning how best to solve a problem that can be recursively decomposed into subproblems in multiple ways.

II. There can be more than one decompositions of the same problem. We have to decide which is the best way to decompose the problem so that the total solution or cost of the solution is good.

III. Examples:

a. Matrix Multiplication

b. Towers of Hanoi

c. Blocks World Problem

d. Theorem Proving

IV. Formulations: (AND/OR Graphs)

a. An OR node represents a choice between possible decompositions.

b. An AND node represents a given decomposition.

The AND-OR graph (or tree) is useful for representing the solution of problems that can be solved by decomposing them into a set of smaller problems, all of which must then be solved. This decomposition or reduction generate arcs that we call AND arcs.

One AND arc may point to any number of successors nodes all of which must be solved in order for the arc to point to a solution. Just as in OR graph, several arcs may emerge from a single node, indicating a variety of ways in which the original problem might be solved.

In order to find solutions in an AND-OR graph, we need an algorithm similar to best-first search but with the ability to handle the AND arcs appropriately.

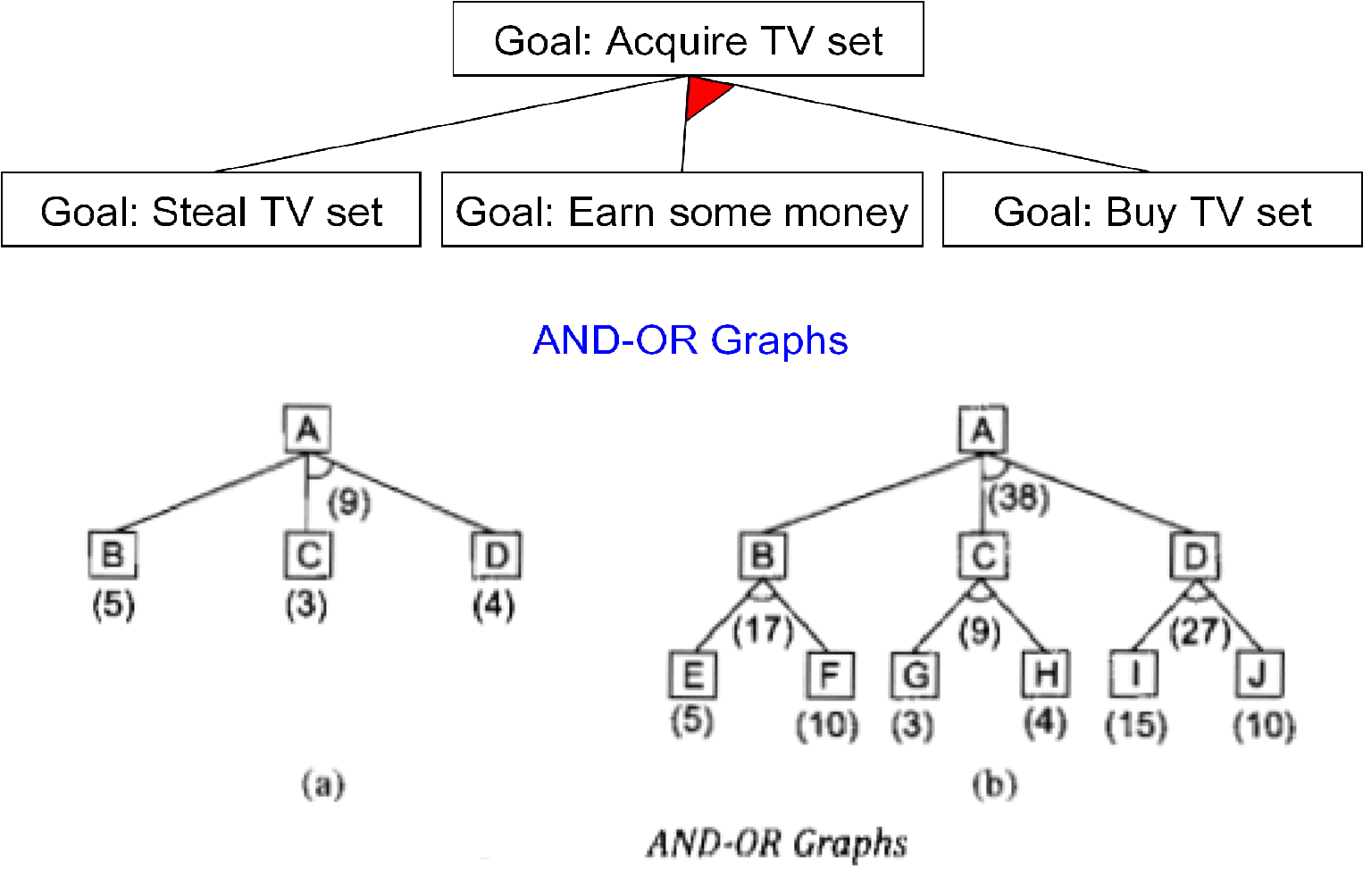
To see why our Best-First search is not adequate for searching AND-OR graphs, consider Fig (a).

I. The top node A has been expanded, producing 2 arcs, one leading to B and one leading to C and D. The numbers at each node represent the value of f' at that node.

II. We assume for simplicity that every operation has a uniform cost, so each arc with a single successor has a cost of 1 and each AND arc with multiple successors has a cost of 1 for each of its components.

III. If we look just at the nodes and choose for expansion the one with the lowest f' value, we must select C. It would be better to explore the path going through B since to use C we must also use D, for a total cost of 9 (C+D+2) compared to the cost of 6 that we get through B.

IV. The choice of which node to expand next must depend not only on the f' value of that node but also on whether that node is part of the current best path from the initial node.

The tree shown in Fig (b)

I. The most promising single node is G with an f' value of 3. It is even part of the most promising arc G-H, with a total cost of 9. But that arc is not part of the current best path since to use it we must also use the arc I-J, with a cost of 27.

II. The path from A, through B, to E and F is better, with a total cost of 18. So we should not expand G next; rather we should examine either E or F.

In order to describe an algorithm for searching an AND-OR graph we need to exploit a value that we call FUTILITY. If the estimated cost of a solution becomes greater than the value of FUTILITY, then we abandon the search. FUTILITY should be chosen to correspond to a threshold such any solution with a cost above it is too expensive to be practical even if it could ever be found.

Algorithm:

1. Initialize the graph to the starting node.

2. Loop until the starting node is labeled SOLVED or until its cost goes above FUTILITY:

a. Traverse the graph, starting at the initial node following the current best path and accumulate the set of nodes that are on that path and have not yet been expanded or labeled solved.

b. Pick up one of those unexpanded nodes and expand it. If there are no successors, assign FUTILITY as the value of this node. Otherwise add the successors to the graph and each of this compute f' (use only h' and ignore g). If f' of any node is "0", mark the node as SOLVED.

c. Change the f' estimate of the newly expanded node to reflect the new information provided by its successors. Propagate this change backward through the graph. If any node contains a successor whose descendants are all solved, label the node itself as SOLVED. At each node that is visible while going up the graph, decide which of its successors arcs is the most promising and mark it as part of the current best path. This may cause the current best path to change. The propagation of revised cost estimates backup the tree was not necessary in the best-first search algorithm because only unexpanded nodes were examined. But now expanded nodes must be reexamined so that the best current path can be selected. Thus it is important that their f' values be the best estimates available.

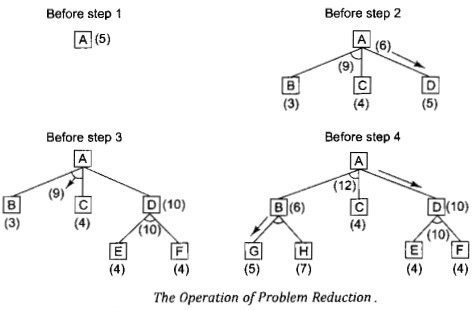
I. At Step 1, A is the only node, so it is at the end of the current best path. It is expanded, yielding nodes B, C and D. The arc to D is labeled as the most promising one emerging from A, since it costs 6 compared to B and C, which costs 9.

II. In Step 2, node D is chosen for expansion. This process produces one new arc, the AND arc to E and F, with a combined cost estimate of 10. So we update the f' value of D to 10.

III. We see that the AND arc B-C is better than the arc to D, so it is labeled as the current best path. At Step 3, we traverse that arc from A and discover the unexpanded nodes B and C. If we are going to find a solution along this path, we will have to expand both B and C eventually. SO explore B first.

IV. This generates two new arcs, the ones to G and to H. Propagating their f' values backward, we update f' to B to 6. This requires updating the cost of AND arc B-C to 12 (6+4+2). Now the arc to D is again the better path from A, so we record that as the current best path and either node E or F will be chosen for the expansion at Step 4.

This process continues until either a solution is found or all paths have led to dead ends, indicating that there is no solution.