we must address several key issues, including the following:

I.

How can the knowledge base be extended to allow inferences to be made on the basis of lack of knowledge as well as on the presence of it?

For example, we would like to be able to say things like, "H you have no reason to suspect that a particular person committed a crime, then assume he didn't," or "If you have no reason to believe that someone is not getting along with her relatives, then assume that the relatives will try to protect her." Specifically, we need to make clear the distinction between:

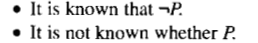
First-order predicate logic allows reasoning to be based on the first of these. We need an extended system that allows reasoning to be based on the second as well. In our new system, we call any inference that depends on the lack of some piece of knowledge a

non-monotonic inference

.

Allowing such reasoning has a significant impact on a knowledge base. Non-monotonic reasoning systems derive their name from the fact that because of inferences that depend on lack of knowledge, knowledge bases may not grow monotonically as new assertions are made. Adding a new assertion may invalidate an inference that depended on the absence of that assertion. First-order predicate logic systems, on the other hand, are monotonic in this respect. As new axioms are asserted, new wff's may become provable, but no old proofs ever become invalid.

II. How can the knowledge base be updated properly when a new fact is added to the system (or when an old one is removed?

In particular, in non-monotonic systems, since the addition of a fact can cause previously discovered proofs to be become invalid, how can those proofs, and all the conclusions that depend on them be found? The usual solution to this problem is to keep track of proofs, which are often called justifications. This makes it possible to find all the justifications that depended on the absence of the new fact, and those proofs can be marked as invalid. Interestingly, such a recording mechanism also makes it possible to support conventional, monotonic reasoning in the case where axioms must occasionally be retracted to reflect changes in the world that is being modelled.

For example, it may be the case that Abbott is in town this week and so is available to testify, but if we wait until next week, he may be out of town. As a result, when we discuss techniques for maintaining valid sets of justifications, we talk both about non-monotonic reasoning and about monotonic reasoning in a changing world.

III.

How can knowledge be used to help resolve conflicts when there are several in consistent non-monotonic inferences that could be drawn?

It turns out that when inferences can be based on the lack of knowledge as well as on its presence, contradictions are much more likely to occur than they were in conventional logical systems in which the only possible contradictions were those that depended on facts that were explicitly asserted to be true. In particular, in non-monotonic systems, there are often portions of the knowledge base that are locally consistent but mutually (globally) inconsistent. As we show below, many techniques for reasoning non-monotonically are able to define the alternatives that could be believed, but most of them provide no way to choose among the options when not all of them can be believed at once.

To do this, we require additional methods for resolving such conflicts in ways that are most appropriate for the particular problem that is being solved, For example, as soon as we conclude that Abbott, Babbitt, and Cabot all claim that they didn't commit a crime, yet we conclude that one of them must have since there's no one else who is believed to have had a motive, we have a contradiction, which we want to resolve in some particular way based on other knowledge that we have.

A different approach and briefly consider what happens if we make fundamental changes to our idea of set membership and corresponding changes to our definitions of logical operations.

The motivation for fuzzy sets is provided by the need to represent such propositions as:

While traditional set theory defines set membership as a Boolean predicate, fuzzy set theory allows us to represent set membership as a possibility distribution, for the set of tall people and the set of very tall people. Notice how this contrasts with the standard Boolean definition for tall people. In the latter, one is either tall or not and there must be a specific height that defines the boundary. The same is true for very tall. In the former, one's tallness increases with one's height until the value of 1 1s reached.

Fuzzy logic is an alternative for representing some kinds of uncertain knowledge. Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. Compared to traditional binary sets (where variables may take on true or false values), fuzzy logic variables may have a truth value that ranges in degree between 0 and 1. Fuzzy logic has been extended to handle the concept of partial truth, where the truth value may range between completely true and completely false. Fuzzy set theory defines set membership as a possibility distribution.

Fuzzy logic is a totally different approach to representing uncertainty:

I. It focuses on ambiguities in describing events rather the uncertainty about the occurrence of an event.

II. Changes the definitions of set theory and logic to allow this.

III. Traditional set theory defines set memberships as a boolean predicate.

The main idea behind semantic nets is that the meaning of a concept comes from the ways in which it is connected to other concepts. In a semantic net, information is represented as a set of nodes connected to each other by a set of labelled arcs, which represent relationships among the nodes. A fragment of a typical semantic net is shown in Fig. 3.1.

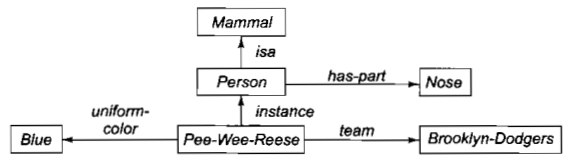
Fig 3.1: A Semantic Network

This network contains examples of both the is a and instance relations, as well as some other, more domain specific relations like ream and uniform-color. In this network, we could use inheritance to derive the additional relation

has-part (Pee-Wee-Reese, Nose)

3.1

Intersection Search

One of the early ways that semantic nets were used was to find relationships among objects by spreading activation out from each of two nodes and seeing where the activation met. This process is called intersection search. Using this process, it is possible to use the network of Fig. 3.1 to answer questions such as "What is the connection between the Brooklyn Dodgers and blue?"! This kind of reasoning exploits one of the important advantages that slot-and-filler structures have over purely logical representations because it takes advantage of the entity-based organization of knowledge that slot-and-filler representations provide.

To answer more structured questions, however, requires networks that are themselves more highly structured. In the next few sections we expand and refine our notion of a network in order to support more sophisticated reasoning.

3.2

Representing Nonbinary Predicates

Semantic nets are a natural way to represent relationships that would appear as ground instances of binary predicates in predicate logic. For example, some of the arcs from Fig. 9.1 could be represented in logic as

But the knowledge expressed by predicates of other arities can also be expressed in semantic nets. We have already seen that many unary predicates in logic can be thought of as binary predicates using some very general-purpose predicates, such as is a and instance. So, for example,

man(Marcus)

could be rewritten as

instance(Marcus, Man)

thereby making it easy to represent in a semantic net.

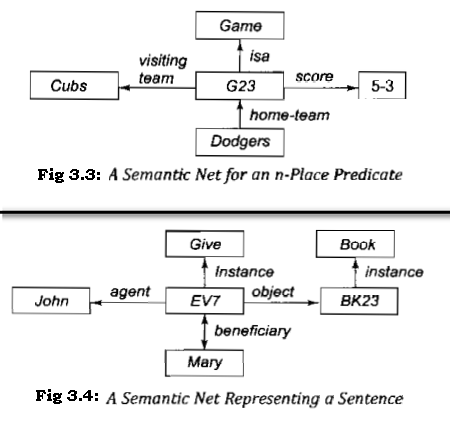
Three or more place predicates can also be converted to a binary form by creating one new object representing the entire predicate statement and then introducing binary predicates to describe the relationship to this new object of each of the original arguments. For example, suppose we know that

score(Cubs, Dodgers, 5-3)

This can be represented in a semantic net by creating a node to represent the specific game and then relating each of the three pieces of information to it. Doing this produces the network shown in Fig. 3.3.

This technique is particularly useful for representing the contents of a typical declarative sentence that describes several aspects of a particular event. The sentence

John gave the book to Mary.

could be represented by the network shown in Fig. 3.4 In fact, several of the earliest uses of semantic nets were in English-understanding programs.

We want to use non-monotonic reasoning to perform what is commonly called default reasoning. two approaches to doing this.

I. Nonmonotonic Logic

II. Default Logic

We then describe two common kinds of nonmonotonic reasoning that can be defined in those logics:

I. Abduction

II. Inheritance

4.1 Nonmonotonic Logic:

One system that provides a basis for default reasoning is Nonmonotonic Logic (NML) [McDermott and Doyle, 1980], in which the language of first-order predicate logic is augmented with a modal operator M, which can be read as "is consistent."' For example, the formula

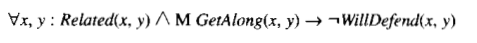
should be read as, "For all x and y, if x and y are related and if the fact that x gets along with y is consistent with everything else that is believed, then conclude that x will defend y."

4.2 Default Logic

An alternative logic for performing default-based reasoning is Reiter's Default Logic (DL) [Reiter, 1980], in which a new class of inference rules is introduced. In this approach, we allow inference rules of the form

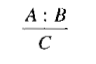
Such a rule should be read as, "If A is provable and it is consistent to assume B then conclude C." As you can see, this is very similar in intent to the nonmonotonic expressions that we used in NML. There are some important differences between the two theories, however. The first is that in DL the new inference miles are used as a basis for computing set of plausible extensions to the knowledge base. Each extension corresponds to one maximal consistent augmentation of the knowledge base.

The Logic then admits as a theorem any expression that is valid in any extension. If a decision among the extensions is necessary to support problem solving, some other mechanism must be provided. So, for example, if we return to the case of Dick the Republican. we can compute two extensions, one corresponding to his being a pacifist and one corresponding to his not being a pacifist.