NOTE!
Click on MENU to Browse between Subjects...17CS54 - AUTOMATA THEORY AND COMPUTABILITY
Answer Script for Module 5
Solved Previous Year Question Paper
CBCS SCHEME
AUTOMATA THEORY AND COMPUTABILITY
ATC
[As per Choice Based Credit System (CBCS) scheme]
(Effective from the academic year 2019 -2020)
SEMESTER - V
Subject Code 17CS54
IA Marks 40
Number of Lecture Hours/Week 04
Exam Marks 60
These Questions are being framed for helping the students in the "FINAL Exams" Only
(Remember for Internals the Question Paper is set by your respective teachers).
Questions may be repeated, just to show students how VTU can frame Questions.
- ADMIN
A multi-tape Turing Machine is nothing but a standard Turing Machine with more number of tapes. Each tape is controlled independently with independent read-write head. The pictorial representation of mulu-tape Turing machine is shown in figure below:
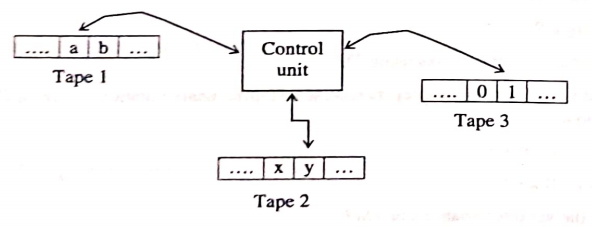
The various components of multi-tape Turing Machine are:
a) Finite control.
b) Each tape having its own symbols and read/write head.
Each tape is divided into cells which can hold any symbol from the given alphabet. To start with the TM should be in start state q0. If the read/write head pointing to tape 1 moves towards night, the read/write head pointing to tape 2 and tape 3 may move towards right or left depending on the transition. The formal definition of Multi-tape Turing machine can be defined as follows.

Where q is the current state. The transition can be interpreted as follows. The TM instate q will be moved to state p only when the first read/write head points to a, the second read-write head points to b and third read/write head points to c and the read/write head will be moved to left in the first case and right in the second case. But, the read/write head with respect to third tape will not be altered. At the same time, the symbols a, b and c will be replaced by x, y and z. It can be easily shown that the n-tape TM in fact is equivalent to the single tape Standard Turing Machine as shown below.
1.a.1 Equivalence of Single Tape and Multi-tape TM's
Theorem: Every language accepted by a multi-tape TM Is recursively enumerable.
Note: The theorem clearly indicates that every language accepted by a multi-tape TM is also accepted by a standard TM.
Proof: This can be shown by simulation. For example, consider a TM with two tapes as shown below:
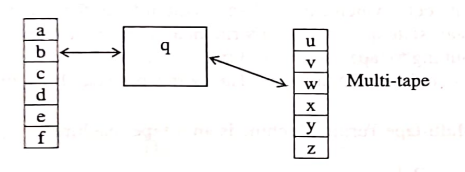
The above 2-tape TMcan be simulated using single tape TM which hasfour tracks as shown in figure below:
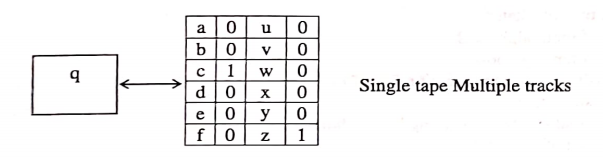
The first and third tracks consist of symbols from first and second tape respectively. The second and fourth track consists of the positions of the read/write head with respect to first and second tape respectively. The value 1 indicates the position of the read/write head. It is clear from the above figure that, the machine in state q and when the first read/write head points to the symbol c, the second read/write head points to the symbol z, then the machine enters into state p, if and only if this transition is defined for TM with multi-tapes. So, whatever transitions have been applied for multi-tape TM, if we apply the same transitions for the new machine that we have constructed, then the two machines are equivalent.
The difference between nondeterministic TM and deterministic TM lies only in the definition of . The formal definition of nondeterministic TM is shown below:

The language is thus set of all those words w in Σ which causes M to move from start state q0 to the final state p.
A nondeterministic TM may have many moves that does not lead to a final state. But, we are interested in only those moves that leads to the final states. The nondeterministic TM in fact is no more powerful than the deterministic TM. Any language accepted by nondeterministic TM can be accepted by deterministic and both are equivalent. We can simulate a deterministic TM from a nondeterministic TM as shown below:
Theorem:
For every nondeterministic TM (NTM)there exists a deterministic TM (DTM)
such that LO(NTM) = L(DTM).
Proof:
Given a string w, NTM starts at the initial configuration (initial ID) and
goes through a sequence of configurations(IDs) until it reaches one of the
conditions:
i. Final state is reached and the machine halts
ii. The transition is not defined and the machine halts
iii. Goes into an infinite loop
To go to the next configuration (ID), the NTM has to choose from finite set of configurations (IDs). All these configurations (IDs) which can be obtained by NTM fora given string w can be represented by a tree. The way NTM is simulated by DTM is shown using the figure shown below:
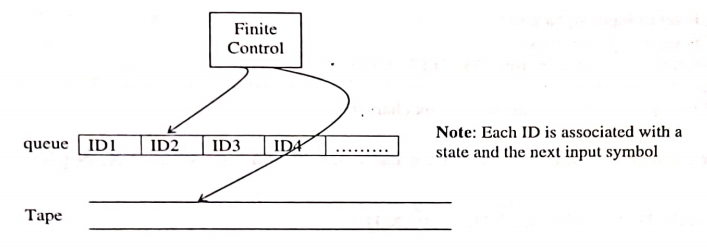
It is clear from the figure that all the IDs of NTM (represented by the nodes of the tree) are placed in the queue one after the other. Each ID inserted into the queue is also associated with the state and the next input symbol to be scanned. The first ID to be explored and examined will be at the front end of the queue. Given any ID in the queue, all IDs to the left of designated ID are assumed to be deleted (marked) and the IDs towards right are assumed to be explored or to be examined. For example, if current ID is ID3 then JD1 and [D2 are already explored and we need not consider them whereas the ID4, IDS, etc., are the nodes to be explored later. The steps carried by DTM are shown below:
Step 1:
The current ID is examined (For the first time current ID is [D1 and is
marked/deleted) based on the state and the scanned symbol. If the state in
the current ID is final state then DTM accepts the string and the machine
halts.
Step 2:
If the state is non final state, the current ID(configuration) is explored
and various IDs(configurations) obtained are inserted at the end of the
queue.
Step 3:
Steps 1 and 2 are repeated until no more ID is examined or queue is empty.
The above steps can be clearly explained using the tree representation. The root node corresponds to the initial configuration (initial ID) and it is the only vertex of level 0. All the configurations (IDs) that are obtained by applying the transition function of NTM only once will be the children of the initial configuration (ID), These new vertices which are derived from the root are at level 1. In general, from the configurations (IDs) at level é, the configurations at level i+1 can be obtained. Since the configurations are finite, the number of children at various levels is finite.
The easiest way to simulate NTM using DTM is to traverse this tree using BFS (Breadth First-Search) from the root until the halt state (the string w is accepted or rejected) is reached. At each level of the tree, the DTM applies the transition function corresponding to the NTM to each configuration (ID) at that level and computes its children (new IDs). These new IDs are the configurations of the next level and they are stored on the tape (if necessary a second tape may be used). If there is a halting state among these children, then DTM accepts the string and halts. It can be easily seen that DTM accepts a string if and only if NTM accepts it. Thus any language accepted by a NTM is also accepted by a DTM.

Definition:
The problems that run forever on a Turing machine are not solvable. In
other words, there are some problem input instances for which Turing
machines will not halt on inputs that they do not accept. Those problems
are called unsolvable or undecidable problems
.
In general, if there is no general algorithm capable of solving every
instance of the problem, then the decision problem is unsolvable
. More precisely, if there is no Turing machine
recognizing the language of all strings for various instances of the
problems input for which the answer is yes or no, then the decision problem
is unsolvable.
Let us assume M is a Turing machine with input alphabets {0, 1}, w is a string of 0's and 1's and M accepts w. If this problem with inputs restricted to binary alphabets {0, 1} is undecidable, then the general problem is undecidable and cannot be solved with a Turing machine with any alphabet.
Note:
The term unsolvable and undecidable are used interchangeably.
Note:
Even though we are able to answer the question in many specific instances,
a problem may be undecidable. It means that there is no single algorithm
guaranteed to provide an answer for every case.
Note:
If a language L is not accepted by a Turing machine, then the language is
not recursively enumerable. One important problem which is not recursively
enumerable that is unsolvable/undecidable decision problem is "Halting
problem".
The "Halting Problem
" can informally be stated as "Given a
Turing machine M and an input string w with the initial configuration q 0, after some (or all) computations do the machine M halts?" In
other words, we have to identify whether (M, w) where M is the Turing
machine, halts or does not halt when w is applied as the input. The domain
of this problem is to be taken as the set of all Turing machines and all w
i.e., Given the description of an arbitrary Turing machine M and the input
string w, we are looking for a single Turing machine that will predict
whether or not the computation of M applied to w will halt.
When we state decidability or undecidability results, we must always know what the domain is, because this may affect the conclusion. The problems may be decidable on some domain but not on another.
It is not possible to find the answer for Halting problem by simulating the action of M on w by a universal Turing machine, because there is no limit on the length of the computation. If M enters into an infinite loop, then no matter how long we wait, we can never be sure that M is in fact in a loop. The machine may be in a loop because of a very long computation. What is required is an algorithm that can determine the correct answer for any M and w by performing some analysis on the machine's description and the input.
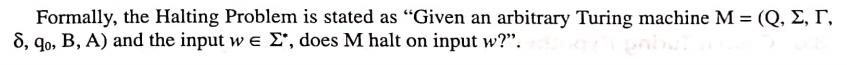
Below Page NAVIGATION Links are Provided...
All the Questions on Question Bank Is SOLVED
Follow our Instagram Page:
FutureVisionBIE
https://www.instagram.com/futurevisionbie/
Message: I'm Unable to Reply to all your Emails
so, You can DM me on the Instagram Page & any other Queries.

 MENU
MENU

