The four informal guidelines that may be used as measures to determine the quality of relation schema design:

i. Making sure that the semantics of the attributes is clear in the schema

ii. Reducing the redundant information in tuples

iii. Reducing the NULL values in tuples

iv. Disallowing the possibility of generating spurious tuples

Guideline 1

: Design a relation schema so that it is easy to explain its meaning. Do not combine attributes from multiple entity types and relationship types into a single relation.

Save storage space and avoid update anomalies.

Insertion anomalies.

Deletion anomalies.

Modification anomalies

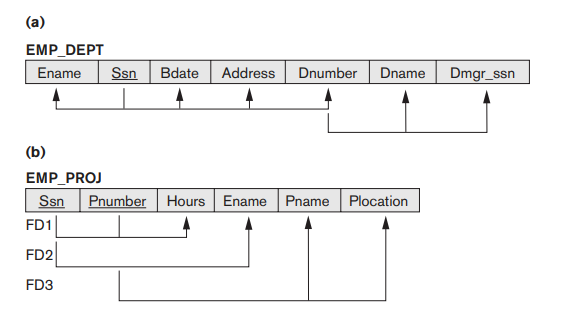
Fig 1.1 Two relation schemas suffering from update anomalies. (a) EMP_DEPT and (b) EMP_PROJ.

Insertion Anomalies

To insert a new employee tuple into EMP_DEPT, we must include either the attribute values for that department that the employee works for, or nulls.

It's difficult to insert a new department that has no employee as yet in the EMP_DEPT relation. The only way to do this is to place null values in the attributes for employee. This causes a problem because SSN is the primary key of EMP_DEPT, and each tuple is supposed to represent an employee entity - not a department entity.

Deletion Anomalies

If we delete from EMP_DEPT an employee tuple that happens to represent the last employee working for a particular department, the information concerning that department is lost from the database.

Modification Anomalies

In EMP_DEPT, if we change the value of one of the attributes of a particular department- say the manager of department 5- we must update the tuples of all employees who work in that department.

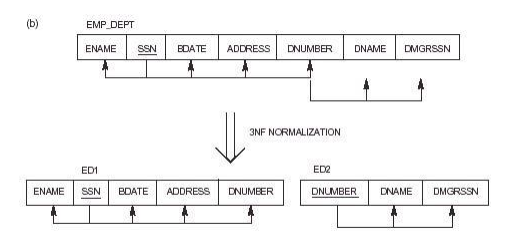
Guideline 2

: Design the base relation schemas so that no insertion, deletion, or modification anomalies occur. Reducing the null values in tuples. e.g., if 10% of employees have offices, it Is better to have a separate relation, EMP_OFFICE, rather than an attribute OFFICE_NUMBER in EMPLOYEE.

Guideline 3

: Avoid placing attributes in a base relation whose values are mostly null. Disallowing spurious tuples.

Spurious tuples

- tuples that are not in the original relation but generated by natural join of decomposed subrelations.

Example: decompose EMP_PROJ into EMP_LOCS and EMP_PROJ1.

Guideline 4

: Design relation schemas so that they can be naturally JOINed on primary keys or foreign keys in a way that guarantees no spurious tuples are generated.

NORMAL FORMS

A relation is defined as a set of tuples. By definition, all elements of a set are distinct; hence, all tuples in a relation must also be distinct. This means that no two tuples can have the same combination of values for all their attributes.

Any set of attributes of a relation schema is called a

superkey

. Every relation has at least one superkey-the set of all its attributes. A

key

is a minimal superkey, i.e., a superkey from which we cannot remove any attribute and still have the uniqueness constraint hold.

In general, a relation schema may have more than one key. In this case, each of the keys is called a

candidate key.

It is common to designate one of the candidate keys as the

primary key

of the relation. A

foreign key

is a key in a relation R but it's not a key (just an attribute) in other relation R' of the same schema.

4.3.1 First Normal Form (1NF)

First normal form is now considered to be part of the formal definition of a relation; historically, it was defined to disallow multivalued attributes, composite attributes, and their combinations. It states that the domains of attributes must include only atomic (simple, indivisible) values and that the value of any attribute in a tuple must be a single value from the domain of that attribute.

Practical Rule: "Eliminate Repeating Groups," i.e., make a separate table for each set of related attributes, and give each table a primary key.

Formal Definition: A relation is in first normal form (1NF) if and only if all underlying simple domains contain atomic values only.

4.3.1 Second Normal Form (2NF)

Second normal form is based on the concept of fully functional dependency. A functional X Y is a fully functional dependency is removal of any attribute A from X means that the dependency does not hold any more. A relation schema is in 2NF if every nonprime attribute in relation is fully functionally dependent on the primary key of the relation. It also can be restated as: a relation schema is in 2NF if every nonprime attribute in relation is not partially dependent on any key of the relation.

Practical Rule: "Eliminate Redundant Data," i.e., if an attribute depends on only part of a multivalued key, remove it to a separate table.

Formal Definition: A relation is in second normal form (2NF) if and only if it is in 1NF and every nonkey attribute is fully dependent on the primary key.

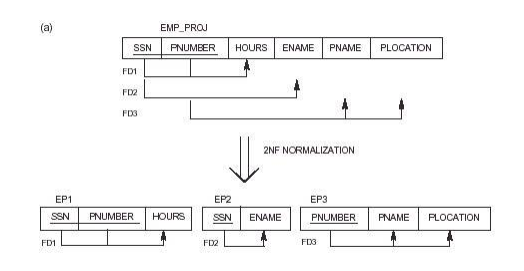
1NF: R is in 1NF iff all domain values are atomic.

2NF: R is in 2 NF iff R is in 1NF and every nonkey attribute is fully dependent on the key.

3NF: R is in 3NF iff R is 2NF and every nonkey attribute is non-transitively dependent on the key.

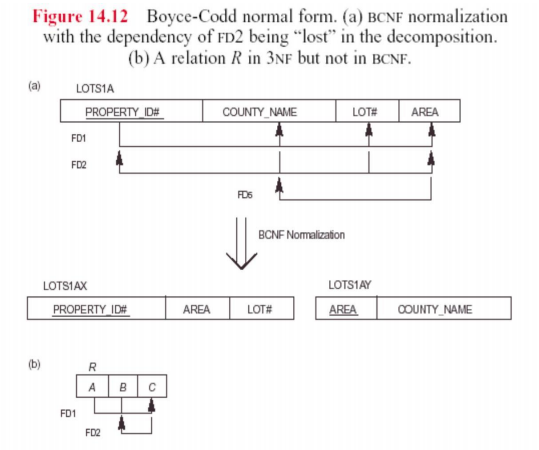
4.3 Boyce-Codd Normal Form (BCNF)

A relation schema R is in Boyce-Codd Normal Form (BCNF) if whenever a FD X -> A holds in R, then X is a superkey of R

· Each normal form is strictly stronger than the previous one:

· Every 2NF relation is in 1NF Every 3NF relation is in 2NF

· Every BCNF relation is in 3NF

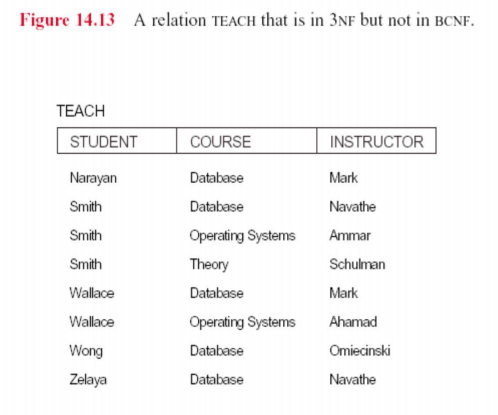
· There exist relations that are in 3NF but not in BCNF

A relation is in BCNF, if and only if every determinant is a candidate key.

Additional criteria may be needed to ensure the the set of relations in a relational database are satisfactory.

Definition. A minimal cover of a set of functional dependencies E is a minimal set of dependencies (in the standard canonical form5 and without redundancy) that is equivalent to E. We can always find at least one minimal cover F for any set of dependencies E using Algorithm 3.1.

Inclusion dependencies were defined in order to formalize two types of interrelational constraints:

a. The foreign key (or referential integrity) constraint cannot be specified as a functional or multivalued dependency because it relates attributes across relations.

b. The constraint between two relations that represent a class/subclass relationship also has no formal definition in terms of the functional, multivalued, and join dependencies.

Inference Rules for Functional Dependencies

We denote by F the set of functional dependencies that are specified on relation schema R. Typically, the schema designer specifies the functional dependencies that are semantically obvious; usually, however, numerous other functional dependencies hold in all legal relation instances among sets of attributes that can be derived from and satisfy the dependencies in F. Those other dependencies can be inferred or deduced from the FDs in F. We call them as inferred or implied functional dependencies

Definition: An FD X → Y is inferred from or implied by a set of dependencies F specified on R if X → Y holds in every legal relation state r of R; that is, whenever r satisfies all the dependencies in F, X → Y also holds in r.

In the following discussion, we use an abbreviated notation when discussing functional dependencies. We concatenate attribute variables and drop the commas for convenience. Hence, the FD {X,Y} → Z is abbreviated to XY → Z, and the FD {X, Y, Z} → {U, V} is abbreviated to XYZ → UV. We present below three rules IR1 through IR3 that are well-known inference rules for functional dependencies. They were proposed first by Armstrong (1974) and hence are known as Armstrong's axioms.

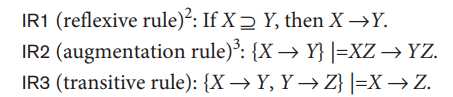
Armstrong has shown that inference rules IR1 through IR3 are sound and complete. By sound, we mean that given a set of functional dependencies F specified on a relation schema R, any dependency that we can infer from F by using IR1 through IR3 holds in every relation state r of R that satisfies the dependencies in F. By complete, we mean that using IR1 through IR3 repeatedly to infer dependencies until no more dependencies can be inferred results in the complete set of all possible dependencies that can be inferred from F. In other words, the set of dependencies F+, which we called the closure of F, can be determined from F by using only inference rules IR1 through IR3.

The reflexive rule (IR1) states that a set of attributes always determines itself or any of its subsets, which is obvious. Because IR1 generates dependencies that are always true, such dependencies are called trivial. Formally, a functional dependency X → Y is trivial if X ⊇ Y; otherwise, it is nontrivial. The augmentation rule (IR2) says that adding the same set of attributes to both the left- and right-hand sides of a dependency results in another valid dependency. According to IR3, functional dependencies are transitive.

Each of the preceding inference rules can be proved from the definition of functional dependency, either by direct proof or by contradiction. A proof by contradiction assumes that the rule does not hold and shows that this is not possible. We now prove that the first three rules IR1 through IR3 are valid. The second proof is by contradiction.

Normalization Algorithms based on FDs to synthesize 3NF and BCNF describe two desirable properties (known as properties of decomposition).

• Dependency Preservation Property
• Lossless join property

Dependency Preservation Property

enables us to enforce a constraint on the original relation from corresponding instances in the smaller relations.

Lossless join property

enables us to fin d any instance of the original relation from corresponding instances in the smaller relations (Both used by the design algorithms to achieve desirable decompositions).

A property of decomposition, which ensures that no spurious rows are generated when relations are reunited through a natural join operation.