1. Explain the general procedure to solve a multistage graph problem using backward approach with an example. (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

2. Construct an optimal binary search tree for the following: (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

Items	A	B	C	D
Probabilities	0.1	0.2	0.4	0.3

3. Design Floyd's algorithm to find shortest distances from all nodes to all other nodes. (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

4. Apply Warshall's algorithm to compute transitive closure for the graph below. (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

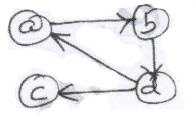
5. Define transitive closure of a directed graph. Find the transitive closure matrix for the graph whose adjacency matrix is given. (10 Marks) (June/July 2019 | 17 Scheme)

6. Find the optimal tour for salesperson using dynamic programming technique. The directed graph is shown in Figure. (10 Marks) (June/July 2019 | 17 Scheme)

7. Write an algorithm to construct optimal binary search tree for the following data: (10 Marks) (June/July 2019 | 17 Scheme)

Key	A	B	C	D
Probability	0.1	0.2	0.4	0.3

8. Apply the bottom-up dynamic programming algorithm to the following instance of the knapsack problem. Knapsack capacity W= 10. (10 Marks) (June/July 2019 | 17 Scheme)

Item	Weight	Value
1	7	42
2	3	12
3	4	40
4	5	25

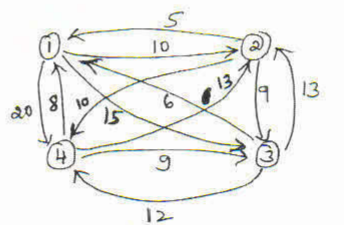
9. Using Floyd's Algorithm solve the all pair shortest path problem for the graph whose weight matrix is given below. (06 Marks) (June/July 2019 | 15 Scheme)

10. Explain Bellman Ford algorithm. (04 Marks) (June/July 2019 | 15 Scheme)

11. State travelling sales person problem. Solve the following using dynamic programming. (06 Marks) (June/July 2019 | 15 Scheme)

12. How would you define Dynamic programming? With an example illustrate multistage graph for forward approach. (06 Marks) (June/July 2019 | 15 Scheme)

13. Using dynamic programming solve the following knapsack n= 4. M=5, (W ₁, W₂, W₃, W₄) = (2, 1, 3, 2). Profit (P₁, P₂, P₃, P₄) =(8, 6, 16, 11). (06 Marks) (June/July 2019 | 15 Scheme)

14. Write Warshall's algorithm. (04 Marks) (June/July 2019 | 15 Scheme)

15. Define transitive closure of a graph. Write Warshall's algorithm to compute transitive closure of a directed graph. Apply the same on the graph defined by the following adjacency matrix: (08 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

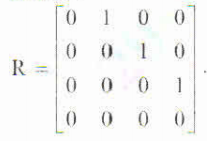
16. Using Dynamic programming, solve the below instance of knapsack problem. Where Capacity w = 5. (08 Marks) (08 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

Items	Weight	Value
1	2	12
2	1	10
3	3	20
4	2	15

17. Obtain an optimal binary search tree for the following four-key set. (08 Marks) (08 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

Key	A	B	C	D
Probability	0.1	0.2	0.4	0.3

18. Solve the following travelling sales person problem represented as a graph shown in Figure using dynamic programming. (08 Marks) (08 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

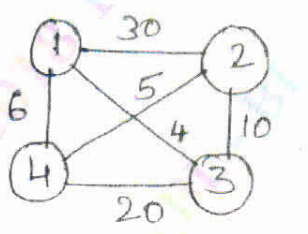
19. Explain multistage graph with an example. Write multistage graph algorithm using backward approach. (08 Marks) (June/July 2018 | 15 Scheme)

20. Apply Floyd's algorithm to solve all pair shortest path problem for the graph given below in Figure (08 Marks) (June/July 2018 | 15 Scheme)

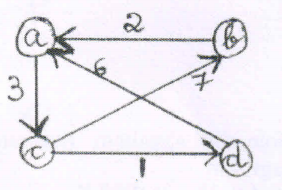
21. Explain Bellman Ford al to find shortest path from single source to all destinations for a directed graph with negative edge cost. (08 Marks) (June/July 2018 | 15 Scheme)

22. Apply Warshall's algorithm to the digraph given below in Figure and find the transitive closure. (08 Marks) (June/July 2018 | 15 Scheme)

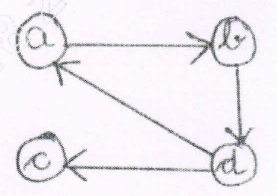
23. Define transitive closure. Write Warshall's algorithm to compute transitive closure. Find its efficiency. (08 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

24. Apply Floyd's algorithm to find all pair shortest path for the graph of Figure. (08 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

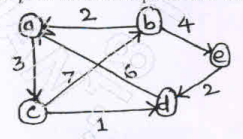
25. For the given cost matrix, obtain optimal cost tour using dynamic programming. (08 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

26. Write a pseudocode to find an optimal binary search tree by dynamic programming. (08 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

27. Explain the concept of dynamic programming, with example. (08 Marks) (June/July 2017 | 15 Scheme)

28. Trace the following graph using Warshall's algorithm. (08 Marks) (June/July 2017 | 15 Scheme)

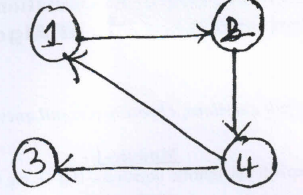
29. Explain Multistage graphs with example. Write multistage graph algorithm to forward approach. (08 Marks) (June/July 2017 | 15 Scheme)

30. Solve the following instance of Knapsack problem using dynamic programming. Knapsack capacity is 5. (08 Marks) (June/July 2017 | 15 Scheme)

Item	Weight	Value
1	2	$12
2	1	$10
3	3	$20
4	2	$15