1. What is Hamiltonian circuit problem? What is the procedure to find Hamiltonian circuit of a graph? (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

2. Explain the classes of NP-Hard and NP-complete. (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

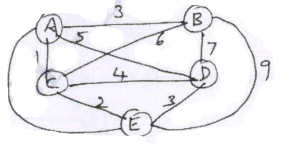
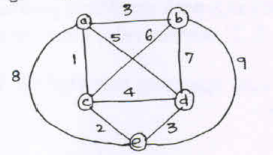
3. Apply the branch and bound algorithm to solve the travelling salesman problem for the graph below. (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

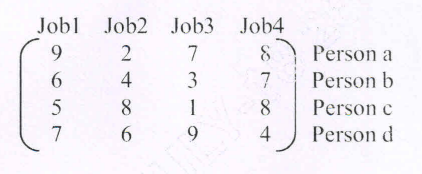
4. Obtain the optimal solution assignment problem given: (10 Marks) (Dec.2019/Jan.2020 | 17 Scheme)

	J1	J2	J3	J4
A	9	2	7	8
B	6	4	3	7
C	5	8	1	8
D	7	6	9	4

5. Construct state-space tree for solving four queen's problem using backtracking. (06 Marks) (June/July 2019 | 17 Scheme)

6. Discuss graph colouring problem. Find different solutions for 4 nodes and all possible 3 colouring problem. (06 Marks) (June/July 2019 | 17 Scheme)

7. Write a note on: (i) Non deterministic algorithms. (ii) LC branch and bound solution to solve O/I knapsack problem. (08 Marks) (June/July 2019 | 17 Scheme)

8. What are the two additional items required by Branch and Bound technique. compared with backtracking. Solve the following assignment problem using branch and bound technique. whose cost matrix for assigning four jobs to four persons are given (10 Marks) (June/July 2019 | 17 Scheme)

9. Discuss the following:

(i) Subset sum problem

(ii) NP hard and NP complete classes. (10 Marks) (June/July 2019 | 17 Scheme)

10. Explain back tracking method? Draw state space tree to generate solutions to 4-Queen's problem. (06 Marks) (June/July 2019 | 15 Scheme)

11. What is branch and bound algorithm? How it is different from backtracking? (04 Marks) (June/July 2019 | 15 Scheme)

12. Define the following :

(i) Class P

(ii) Class NP

(iii) NP complete problem. (06 Marks) (June/July 2019 | 15 Scheme)

13. Apply backtracking technique to solve the instance of the sum of subset problem:

S= {3,5,6,7} and d=15. (08 Marks) (June/July 2019 | 15 Scheme)

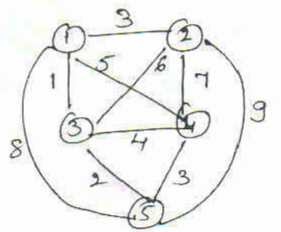
14. Apply branch and bound algorithm to solve the traveling salesman problem for the following graph in Figure. (08 Marks) (June/July 2019 | 15 Scheme)

15. What is the central principle of backtracking? Apply backtracking to solve the below instance of sum of subset problem

S = {5, 10, 12, 13,15, 18} d=30. (08 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

16. Solve the below instance of assignment problem using branch and bound algorithm. (08 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

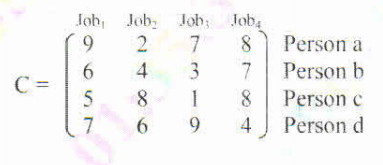
17. Draw the state-space tree to generate solutions to 4-Queen's problem. (04 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

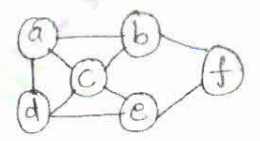
18. Apply backtracking to the problem of finding a Hamiltonian circuit m the graph shown below: (04 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

19. Define the following:

i) Class P

ii) Class NP

iii) NP complete problem

iv) NP hard problem. (08 Marks) (Dec.2018/Jan.2019 | 15 Scheme)

20. Apply backtracking method to solve subset-sum problem for the instance d = 30 and S = {5, 10, 12, 13, 15, 18}. Give all possible solutions. (08 Marks) (June/July 2018 | 15 Scheme)

21. Explain how travelling salesman problem can be solved using branch and bound technic. (06 Marks) (June/July 2018 | 15 Scheme)

22. Define deterministic and non-deterministic algorithms. (02 Marks) (June/July 2018 | 15 Scheme)

23. What is Hamiltonian cycle? Explain the algorithm to find the Hamiltonian cycle in a given connected graph. Write the functions used for generating next vertex and for finding Hamiltonian cycles. (09 Marks) (June/July 2018 | 15 Scheme)

24. Apply the best-first branch-and-bound algorithm to solve the instance of the given job assignment problem. (07 Marks) (June/July 2018 | 15 Scheme)

25. Write the pseudocode for backtracking algorithm. Let w = {3, 5, 6, 7} and m= 15. Find all possible subsets of w that sum to m. Draw the state space tree that is generated. (09 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

26. Draw the portion of the state space tree for m colourings of a graph when n = 4 and m= 3. (07 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

27. With the help of a state space tree. solve the Travelling Salesman Problem (TSP) of Figure, using branch-and-bound algorithm. (08 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

28. Explain the classes of NP Hard and NP complete. (08 Marks) (Dec.2017/Jan.2018 | 15 Scheme)

29. Explain backtracking concept. Illustrate N queens problem using backtracking to solve 4-Queens problem. (08 Marks) (June/July 2017 | 15 Scheme)

30. Solve subset sum problem for the following example, s = {3, 5, 6, 7} and d= 15. Construct a state space tree. (08 Marks) (June/July 2017 | 15 Scheme)

31. Explain the concept of branch and bound and solve assignment problem for the following and obtain optimal solution. (08 Marks) (June/July 2017 | 15 Scheme)

32. Explain LC Branch and Bound and FIFO branch and bound. (08 Marks) (June/July 2017 | 15 Scheme)