1. What is clipping? Explain with example the Sutherland-Hodgman polygon clipping algorithm. (08 Marks) (Dec.2019/Jan.2020)

2. Explain basic illumination models. (08 Marks) (Dec.2019/Jan.2020)

3. Explain RGB and CMY color models with examples. Explain the transformation between CMY and RGB color spaces. (08 Marks) (Dec.2019/Jan.2020)

4. Obtain the matrix representation for rotation of a object about an arbitrary axis. (08 Marks) (Dec.2019/Jan.2020)

---

---

5. Design a transformation matrix for window to viewport transformation. And explain how reshape function (glutReshapeFunc) works in openGL programming. (05 Marks) (June/July 2019)

6. With the help of a suitable diagram explain basic 3D Geometric transformation techniques and give the transformation matrix. Explain the meaning of affine transformation. (05 Marks) (June/July 2019)

7. With the help of openGL statements and diagram explain illumination and shading models. (06 Marks) (June/July 2019)

8. What is Clipping? With the help of a suitable example explain cohen Southerland line clipping algorithm. (06 Marks) (June/July 2019)

---

---

9. Design transformation matrix to rotate an 3D object about an axis that is parallel to one of the co-ordinate axes. (06 Marks) (June/July 2019)

10. With the help of a suitable diagram, explain basic illumination, RGB and CMY colour models. (04 Marks) (June/July 2019)

11. Define clipping. Briefly explain Co-hen Suterland line clipping without code. Discuss four cases. (10 Marks) (Dec.2018/Jan.2019)

12. Describe phong lighting model. (06 Marks) (Dec.2018/Jan.2019)

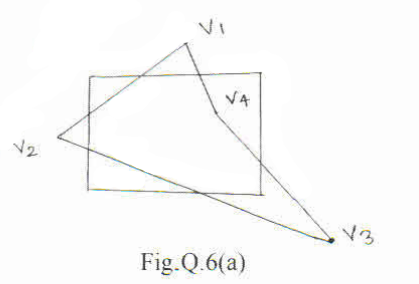
13. Clip the polygon given in Fig.Q.6(a), using Suterland Hodgman polygon clipping algorithm with neat sketches. (06 Marks) (Dec.2018/Jan.2019)

---

---

14. Explain the different types of light sources supported by OpenGl. (06 Marks) (Dec.2018/Jan.2019)

15. Explain the RGB and CMY color models. (04 Marks) (Dec.2018/Jan.2019)

16. Explain Cohen Sutherland line clipping clip the lines with coordinates (x₀, y₀) = (60, 20) (x₁, y₁) = (80, 120) given the window boundaries (X_wmin, Y_wmin) = (50, 50) and (X_wmax, Y_wmax) = (100, 100) (08 Marks) (June/July 2018)

17. Define color model. With neat diagram explain RGB and CMY color model. (08 Marks) (June/July 2018)

18. Explain Sutherland Hodgman Polygon clipping. Find the final clipped vertices for the following Fig Q6(a) (08 Marks) (June/July 2018)

---

---

19. Explain Specular Reflection and phong model. (08 Marks) (June/July 2018)

20. Define and represent the following #D transformation in homogeneous co-ordinates system:

I. Translation

II. Scaling (Dec.2016/Jan.2017 |10 Scheme)

21. What is concatenation of transformation? Explain 3D rotation about a fixed point. (10 Marks) (Dec.2016/Jan.2017 |10 Scheme)

---

---

22. Bring out the differences between perspective and parallel projections. (6 Marks) (Dec.2016/Jan.2017 |10 Scheme)

23. Explain the 2-buffer algorithm. (04 Marks) (Dec.2016/Jan.2017 |10 Scheme)

24. Derive the simple perspective projection matrix. (10 Marks) (Dec.2016/Jan.2017 |10 Scheme)

25. What care Affine transformation? Explain the basic affine transformation in 3D along with their matrix forms. (10 Marks) (June/July.2019 |10 Scheme)

26. What care Quaternions? With an example. explain how Quaternion are used in rotation in a 3D space. Give the mathematical representation of Quaternion. (10 Marks) (June/July.2019 |10 Scheme)

27. What are simple projections? Obtain perspective and orthogonal 4x4 matrix representation. (10 Marks) (June/July.2019 |10 Scheme)

28. Briefly explain the projections in openGL and demonstrate with the help of a suitable program. (10 Marks) (June/July.2019 |10 Scheme)

---

---

29. What is concatenation transformation? Explain rotation about a fixed point. (08 Marks) (Dec.2017/Jan.2018 |10 Scheme)

30. Explain how quaternions are used in rotation in a three-dimensional space. also list some of its advantages. (12 Marks) (Dec.2017/Jan.2018 |10 Scheme)

31. Explain the various types of views that are employed in computer graphics systems. (10 Marks) (Dec.2017/Jan.2018 |10 Scheme)

32. Explain glFrustrum( ) with syntax. (06 Marks) (Dec.2017/Jan.2018 |10 Scheme)

33. Define the term Axonometric projection, also list its types. (04 Marks) (Dec.2017/Jan.2018 |10 Scheme)

34. Obtain the matrix representation for rotation of a point about an arbitrary axis in a 3D space. (10 Marks) (June/July.2017 |10 Scheme)

---

---

35. Show that the following three dimensional sequences are commute:

I. A rotation and a uniform scaling.

II. Two rotations about the same axis. (10 Marks) (June/July.2017 |10 Scheme)