×
NOTE!
Click on MENU to Browse between Subjects...
Advertisement
COMPUTER GRAPHICS LABORATORY WITH MINI PROJECT
[As per Choice Based Credit System (CBCS) scheme]
(Effective from the academic year 2017 - 2018)
SEMESTER - VI
Subject Code 17CSL68
IA Marks 40
Number of Lecture Hours/Week 01I + 02P
Exam Marks 60
Advertisement
17CSL68 - COMPUTER GRAPHICS LABORATORY WITH MINI PROJECT
PROGRAM - 7
Design, develop and implement recursively subdivide a tetrahedron to form 3D sierpinski gasket. The number of recursive steps is to be specified by the user.
Code Credits Prof Shankar R, BMSIT
DESIGN Credits Mr K B Hemanth Raj - Admin
Advertisement
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 | #include<stdlib.h> #include<stdio.h> #include<GL/glut.h> typedef float point[3]; point v[]= {{0, 0, 1}, {0, 1, 0}, {-1, -0.5, 0}, {1, -0.5, 0}}; int n; void triangle(point a,point b,point c) { glBegin(GL_POLYGON); glVertex3fv(a); glVertex3fv(b); glVertex3fv(c); glEnd(); } void divide_triangle(point a,point b,point c,int n) { point v1,v2,v3; int j; if(n>0) { for(j=0; j<3; j++) v1[j] = (a[j]+b[j])/2; for(j=0; j<3; j++) v2[j] = (a[j]+c[j])/2; for(j=0; j<3; j++) v3[j] = (c[j]+b[j])/2; divide_triangle(a,v1,v2,n-1); glFlush(); divide_triangle(c,v2,v3,n-1); glFlush(); divide_triangle(b,v3,v1,n-1); glFlush(); } else(triangle(a,b,c)); } void tetrahedron(int n) { glColor3f(1, 0, 0); divide_triangle(v[0], v[1], v[2], n); glColor3f(0, 1, 0); divide_triangle(v[3], v[2], v[1], n); glColor3f(0, 0, 1); divide_triangle(v[0], v[3], v[1], n); glColor3f(0, 0, 0); divide_triangle(v[0], v[2], v[3], n); } void display(void) { glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT); glLoadIdentity(); tetrahedron(n); glFlush(); } void myReshape(int w,int h) { glViewport(0, 0, w, h); glMatrixMode(GL_PROJECTION); glLoadIdentity(); if(w<=h) glOrtho(-2, 2, -2*(GLfloat)h/(GLfloat)w, 2*(GLfloat)h/(GLfloat)w, -10, 10); else glOrtho(-2*(GLfloat)w/(GLfloat)h, 2*(GLfloat)w/(GLfloat)h, -2, 2, -10, 10); glMatrixMode(GL_MODELVIEW); glutPostRedisplay(); } int main(int argc,char ** argv) { printf("No of Recursive steps/Division: "); scanf("%d",&n); glutInit(&argc,argv); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB|GLUT_DEPTH); glutCreateWindow(" 3D Sierpinski gasket"); glutReshapeFunc(myReshape); glutDisplayFunc(display); glEnable(GL_DEPTH_TEST); glClearColor(1, 1, 1, 0); glutMainLoop(); return 0; } |
Advertisement
Input the Number of N
n==2
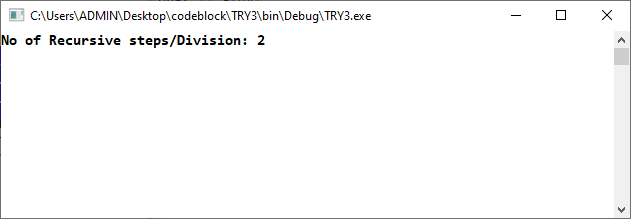
Fig 1.1: n==2 shell prompt .
Advertisement
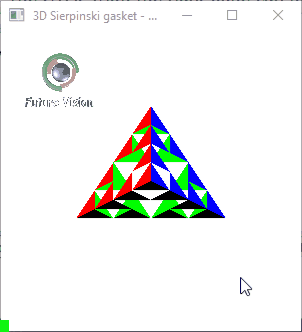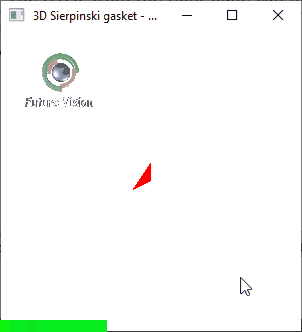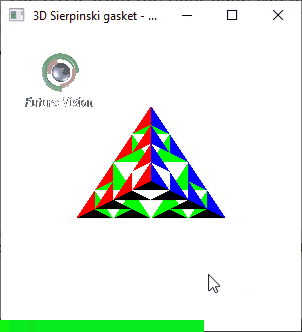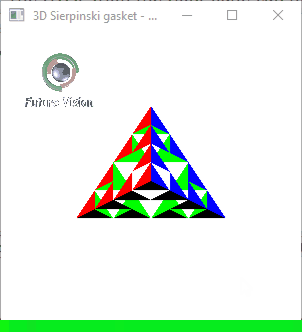
Fig 1.2: n==2 Animated output .
Input the Number of N
n==3
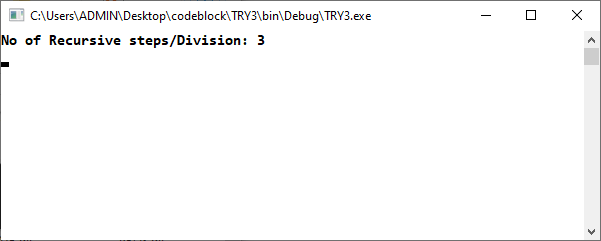
Fig 1.3: n==3 shell prompt .
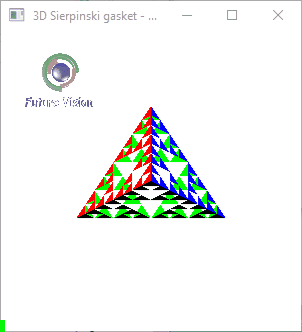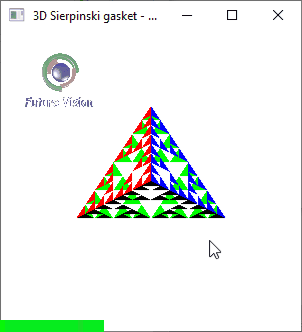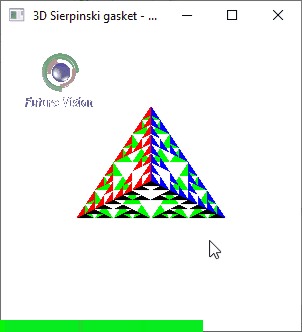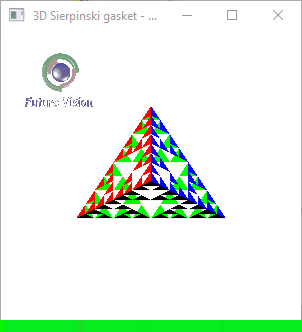
Fig 1.4: n==3 Animated output .
Input the Number of N
n==5
Advertisement
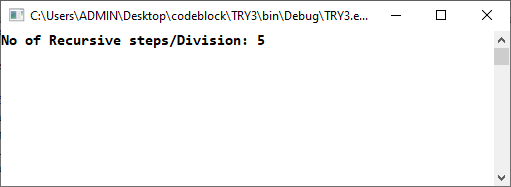
Fig 1.5: n==5 shell prompt .
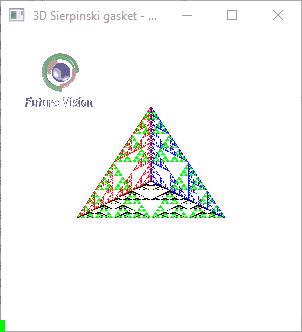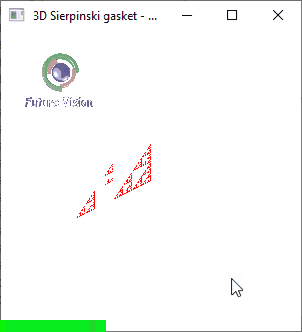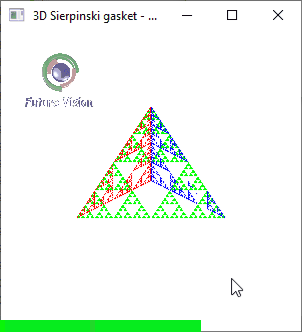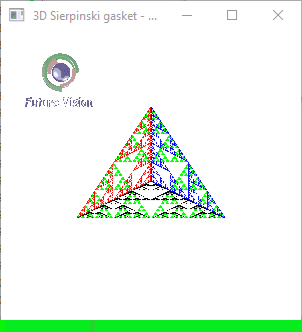
Fig 1.6: n==5 Animated output .
×
Note
Please Share the website link with Your Friends and known Students...
-ADMIN
-ADMIN
×
Note
Page Number is specified to navigate between Pages...
T = Text book
QB = Question Bank
AS = Amswer Script
-ADMIN
T = Text book
QB = Question Bank
AS = Amswer Script
-ADMIN
Advertisement

 MENU
MENU

